The Mathematics of Ancient Egypt

Much is made of the Greek contribution to mathematics, and rightfully so. Euclid’s Elements, for example, is both the culmination of a great tradition (starting, let’s say, with Thales) as well as the starting point for mathematics-as-mathematicians-know-it.

However. the Greeks drew upon the mathematics of older cultures, particularly the Egyptians and Babylonians. This can be ascertained from archeological evidence such as the famous “Plimpton 322” Babylonian tablet of Pythagorean triples. And the Greeks themselves credit the Egyptians for the creation of geometry. However, the Egyptian contribution to mathematics is not so well understood by today’s general mathematical audience.

Mathematical Papyri

One of the reasons for this is that, relative to Greece, there is significantly less source material of Egyptian mathematics to work with. This is partly because ancient Egypt is just so, well, ancient. The first dynasty (after lower and upper Egypt were unified) starts roughly 3100 BC. The pyramids at Giza were built around 2600 BC. Our best mathematical source, the Rhind papyrus (named after the Scottish lawyer who purchased it in Luxor, formerly ancient Thebes), dates to around 1600 BC.

The Rhind Papyrus is essentially an exercise book for Royal scribes in training. It begins thus:

“Accurate reckoning. The entrance into the knowledge of all existing things and all obscure secrets. This book was copied in the year 33, in the fourth month of the inundation season, under the majesty of the king of Upper and Lower Egypt, ‘A-user-Re’, endowed with life, in likeness to writings of old made in the time of the king of Upper and Lower Egypt, Ne-ma’et-Re’. It is the scribe Ahmes who copies this writing.”

So what was the mathematics of ancient Egypt like?

Mostly I’ll be concerned with arithmetic, as found in the Rhind papyrus.

Egyptian Numerals

Numbers could be naturally expressed via hieroglyphics, with a few basic symbols denoting quantities at various orders of magnitude, and with the grouping of symbols corresponding to addion.

Hieroglyphic	Arabic Numeral
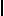	1
	10
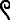	100
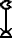	1,000
	10,000
	100,000
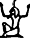	1,000,000

Thus is the number 12. Addition of two numbers in this notation is in a sense trivial, but can quickly grow unwieldy ¹.

Multiplication

So how does multiplication work? For what follows we stick with ordinary Hindu-Arabic numerals, but nonetheless work in the Egyptian style.

Consider for example the product \(12 \times 12\) ². Form a table, starting with

1	12

and then repeatedly doubling to get new entries:

1	12
2	24
4	48
8	56

We find rows for which the left column sums to 12 (indicated by ‘→’):

	1	12
	2	24
→	4	48
→	8	56

and the value of the product is the sum of these rows in the right column, namely \(48 + 56 = 144\). This is similar to the “Russian peasant” method of multiplication.

Strictly speaking, one can use any convenient or known product to add a row to the table. As a quick example, consider \(16 \times 16\):

→	1	16
→	10	160
→	5	80

which reveals that the sum is \(16 + 160 + 80 = 256\). In this example, the third row is obtained from the second by halving.

Division without remainder

Division works similarly, albeit with a bit more guesswork. To compute \(90 / 5\), one multiplies 5 until 90 is obtained.

	1	5
→	2	10
→	4	20
→	8	50

This time, the quotient is the sum in the left column: \(2 + 4 + 8 = 14\).

Fractions

Division with remainder is where things start getting interesting. The ancient Egyptians had a restricted notion of fractional numbers, specifically a “part” out of some number of parts. That is to say, they had a notation for the numbers \(1/n\) (a “unit fraction”). The hieroglyphic symbol for \(1/n\) was formed by placing an open mouth over the symbol for \(n\), as in (denoting \(1/3\)). Aside from these numbers, the only other fraction which they could express immediately was \(2/3\), written as All other fractions were represented as sums of these.

In order for the Egyptian scribes to work with unit fractions effectively, they must be able to quickly recognize and recall certain identities. Some of the simplest ones are as follows:

\(1/3 + 1/6 = 1/2\)

\(1/2 + 1/3 + 1/6 = 1\)

\(2/3 = 1/2 + 1/6\)

(recall that even though \(2/3\) is not a unit fraction, it did have a hieroglyph).

Consider now the problem of division with remainder. As an example, let’s compute \(19 / 8\) using the Egyptian method. One begins as with any division problem, forming a table as such:

1	8
2	16

At this point, we have \(2 \cdot 8 = 16\), so there is a remaining quantity of \(19 - 16 = 3\) to be accounted for. This is not an integer multiple of \(8\), so we rely on fractions:

	1	8
→	2	16
→	\(1/2\)	4
→	\(1/4\)	2
→	\(1/8\)	1

Thus we began with repeated doubling, and then proceeded by repeated halving to get \(19 = (2 + 1/4 + 1/8) \cdot 8\).

Doubling unit fractions

We can see then that doubling and halving are basic arithmetic operations, essential to performing more complicated multiplications and divisions. A weakness of the notation is that under repeated doublings it quickly becomes tedious to express fractions. Naively speaking, \(1/7\) doubled once is \(1/7 + 1/7\), and then doubled again is \(1/7 + 1/7 + 1/7 + 1/7\). Consider drawing the equivalent hieroglyphics: there are four mouths and 28 vertical strokes! Thus the Egyptians preferred to simplify fractions into sums of larger unit fractions, so that \(4/7 = 1/2 + 1/14\).

But how would this be computed?

The easiest fraction to double is one where the denominator is divisible by \(2\). So, for example, doubling \(1/4\) yields \(1/2\).

The next easiest case is when the denominator is a multiple of \(3\). Here we may resort to the following set of identities, obtained from the relation \(2/3 = 1/2 + 1/6\) by multiplying by \(1/2, 1/3, 1/4, \ldots\):

\(1/3 + 1/3 = 1/2 + 1/6\)

\(1/6 + 1/6 = 1/4 + 1/12\)

\(1/9 + 1/9 = 1/6 + 1/18\)

\(1/12 + 1/12 = 1/8 + 1/24\)

and so on. The left hand side expresses a doubled fraction, the right hand side expresses its simplified form.

In order to double fractions with denominators not divisible by \(2\) or \(3\), one resorts to the following:

To double \(1/n\), divide \(2\) by \(n\).

This is a major theoretical device in Egyptian arithmetic, and the power of \(2/n = 2 \cdot (1/n)\) is a bit obscured by our modern notation (which is designed to make such identities look trivial). Needless to say, if you were doing mathematics with hieroglyphic or hieratic notation it would not be so obvious.

Thus for example, the double of \(1/5\) is found by

	1	5
	\(2/3\)	\(3 + 1/3\)
→	\(1/3\)	\(1 + 2/3\)
→	\(1/15\)	\(1/3\)

yielding \(1/5 + 1/5 = 1/3 + 1/15\).³

Such computations were so essential to Egyptian arithmetic that in fact the Rhind papyrus begins with a list of computations giving \(2\) divided by all odd divisors from \(2/3\) to \(2/101\) !

A few other remarks

The ancient Egyptians were a practical people, with scribes concerned with the practical affairs of engineering and accounting. The emphasis in this discussion has been primarily on arithmetic, in part because this seems to be the emphasis of the remaining papyri.

But what else can we say about Egyptian mathematics? I will not go into detail here, beyond pointing out that the ancient Egyptians did have a primitive notion of algebra (in the form of certain word problems which amount to solving a single linear equation, but without algebraic notation), and that they also knew formulas for certain basic areas and volumes. One of the more impressive accomplishments is the Egyptian approximation $π ≈ (16/9)² = 3.16049…$, which was a much more accurate approximation than the Babylonian \(\pi \approx 3\).

References

1. van der Waerden, Science Awakening.
2. Joseph, The Crest of the Peacock.
3. Chace, The Rhind Mathematical Papyrus: Free Translation and Commentary with Selected Photographs, Translations, Transliterations and Literal Translations.

For a more involved discussion, I can recommend the book “Science Awakening” by van der Waerden, as well as the more recent “The Crest of the Peacock” by Joseph.

Footnotes

Site generated by Hakyll